For an introduction to gravitational waves, see here.
Before 2016, a nobel prize had already been rewarded for an observation that was consistent with, and seemed to confirm, the existence of gravitational waves. In 1974, Russell Hulse and Joesph Taylor discovered a very compact binary system of objects at a distance of 21,000 light years, consisting of two neutron stars orbiting one another. One of the bodies was also a pulsar, meaning that the radiation beams emitted from its poles periodically point toward Earth as it rotates. Since the rotation rate of a neutron star changes only very slowly over time, pulsars are fairly precise clocks. However, Hulse and Taylor detected that the pulses did not reach Earth precisely on time, but varied slightly from the expected arrival time. They were sometimes sooner, sometimes later in a regular pattern, indicating that the pulsar in question was in fact part of a binary system.
The above diagram depicts the binary system consisting of pulsar B1913+16 and its companion, another neutron star. No radiation from the companion has been observed on Earth, indicating that its poles oriented away from us. However, its presence can be inferred from the fact that the pulsar moves farther and closer to Earth in a short, regular period, indicating an orbit. The difference in arrival times is about 3 seconds, indicating that the orbit is about 3 light-seconds across. Further, the orbital period is 7.75 hours.
This discovery provided an excellent opportunity to confirm the predictions of general relativity: such a compact system with rapidly orbiting masses would radiate fairly large quantities of gravitational radiation. However, direct detection was well beyond 1970's technology. Instead, Taylor observed the pulsar system over a number of decades, and found the following:
Since the discovery of the pulsar, its orbital period had been decreasing very slowly, though steadily and measurably, by about 35 seconds over a timespan of 30 years. This is very little relative to the total period of 7.75 hours, but the data matched the predictions of general relativity almost precisely: as energy was lost to gravitational waves, the neutron stars gradually spiral inward toward one other as their orbits becoming shorter and shorter. This remarkable confirmation of a prediction of relativity won Hulse and Taylor the Noble Prize in physics in 1993.
And there the matter sat. Though detectors grew more and more advanced, no direct detections of gravitational waves were made for over 20 years. This all changed in 2015.
On September 14, 2015, at 09:50:45 UTC, shortly after LIGO (the Laser Interferometer Gravitational-Wave Observatory) resumed activity following an upgrade, the two detectors in Washington State and Louisiana picked up a transient gravitational wave signal, the first ever observed by humankind. The announcement of the discovery was made several months later, on February 11, 2016.
The above image shows the signals recorded at Hanford, Washington (left) and Livingston, Louisiana (right). The signals are also superimposed on the right to demonstrate their similarity. The horizontal axis is time, measured relative to 09:50:45 UTC on that day. The reader may notice that the event was distinguishable from the surrounding noise in the detector for only about 0.05 seconds (the third row charts the residual noise after the theoretical waveform in the second row is subtracted out). The final row shows the rapid increase in gravitational wave amplitude during the event and the subsequent silence. The vertical dimension in the first several rows is the relative strain on the detectors, or the amount by which the different arms of LIGO were stretched or compressed by the ripples in spacetime. The scale for these axes measures strain by parts in 10-21. This corresponds to extraordinarily minute changes in length: the 4 kilometer arms of the LIGO detector changed by only about 10-18 meters, only about one thousandth the diameter of a proton!
The theoretical wave form above was a simulation of the event that generated the gravitational waves: the final in-spiraling and ultimate merging of two black holes. The increasing frequency and amplitude of the signals corresponds to the final moments of the collapsing system as the two black holes orbit faster and faster and tighter and tighter around one another before finally combining. Further, the signals at the two detectors were separated by 6.9 ms, smaller than the light travel time between the sites of 10 ms. The delay between the arrival times allows the direction of the source to be identified.
This image shows the region in the sky from which the signals likely originated. The colors indicate the confidence that the source lay within the indicated region: purple is the 90% confidence region and yellow the 50% confidence region. The uncertainty arises from the fact that there were two detectors, and not the three required for a full triangulation.
In addition to the location of the source, the analysis of the waveform yields more. The distance of the system was roughly 1.2 billion light-years, meaning that the merger that we are just now observing occurred over a billion years ago. The two black holes had respective masses of about 36 and 29 solar masses, while the final black hole after the merger weighed in at 62 solar masses. This corresponds to a loss of about 3 solar masses, which was all converted into energy released as gravitational waves as the holes merged. The magnitude of this cataclysm can scarcely be overstated: at its peak, the rate of energy release was an estimated 3.6x1049 W, greater than the radiation emitted from all stars in the observable universe combined!
In addition to being a resounding confirmation of general relativity, the observation was the first truly direct detection of black holes: the fact that such massive objects came within hundreds of kilometers of one another indicates that they had extremely high densities, densities only possible in black holes. But while significant, cosmologists were already nearly certain that both gravitational waves and black holes existed. However, this discovery marks the opening of a brand new field of astronomy. Gravitational waves, which pass unimpeded through nearly anything over nearly any distance, allow us to "hear" cosmic events that we could not have detected before. In theory, these waves could allow us to observe the earliest stages of the universe, before it became transparent to electromagnetic radiation. In 2016, 100 years after Einstein predicted gravitational waves, we took the first step towards seeing the universe in a new way.
Sources: http://articles.adsabs.harvard.edu/cgi-bin/nph-iarticle_query?1989ApJ...345..434T&data_type=PDF_HIGH&whole_paper=YES&type=PRINTER&filetype=.pdf, https://journals.aps.org/prl/pdf/10.1103/PhysRevLett.116.061102, http://resources.edb.gov.hk/physics/articlePic/InterestingTopics/BinaryStars_pic04E.gif
Saturday, February 20, 2016
Friday, February 12, 2016
The Projective Plane: A Visual Introduction
The statement "any two distinct lines intersect in a point" is almost true in normal plane geometry. The exception, of course, is the case of two parallel lines. However, from real experience we know from the rules of perspective that two parallel lines "converge" very far away, even if we know that they in fact maintain the same distance apart.
From this, we naturally comes the intuition that "parallel lines intersect at infinity." Certainly this tidies up our intersection statement because it provides a way for even parallel lines to intersect. But what does "at infinity" mean? Is there really a "point" there? The notion of projective space makes these ideas explicit and rigorous.
We focus on the (real) projective plane, the extension of the normal plane to include these "points at infinity" where parallel lines intersect. The set of points in the projective plane is defined, somewhat enigmatically, as "the set of lines through the origin in three-dimensional space." Defining each point to be a line in a different space seems extremely confusing at first, but there are multiple ways to visualize this concept.
The first method of visualization illustrates how the projective plane is related to the ordinary plane (sometimes called the affine plane). Consider three-dimensional space with ordinary coordinates x,y, and z as shown. The plane labeled z = 1 contains all points for which the z coordinate is 1, namely all those of the form (x,y,1). Clearly this plane is just like the ordinary two-dimensional plane (under the correspondence (x,y,1) → (x,y)), only embedded in three dimensions, like a flat sheet of paper in our world (but infinite). The dotted line shown that passes through the origin intersects the plane at the particular point (a,b,1). Remembering that the projective plane is meant to be an extension of the affine plane, we identify the dotted line with the point where it intersects the plane. Clearly, for each point in the z = 1 plane, there exists exactly one line through the origin and the given point. This shows how the ordinary plane is a subset of projective space (the set of lines through the origin)!
However, not every line through the origin intersects the plane z = 1. For instance, the x-axis, the y-axis (both shown), and any other line in the plane of these two axes only contain points for which the z coordinate is 0 and can never intersect the plane z = 1 (to be clear, the three-dimensional space considered here does not have its own points at infinity!). Therefore, these lines cannot correspond to points on the ordinary plane. These special lines, in fact, are the points at infinity in the projective plane.
The above visualization illustrates the connection between the projective plane and the affine plane. It also indicates that there are many points at infinity, one for each line through the origin "lying flat" in the xy-plane. However, it fails to indicate how points at infinity are truly the intersections of parallel lines. For this, we use another visualization that chooses different representative points.
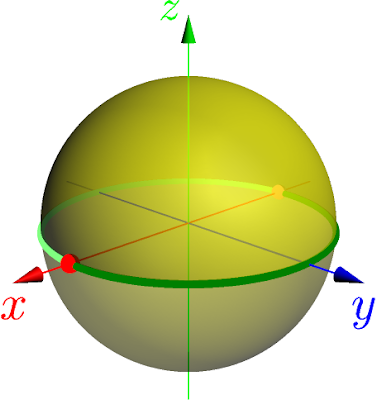
Using a sphere (or a hemisphere, to be more precise) to represent the projective plane is just as legitimate as using a plane: all that matters is that there is one point for each line through the origin. It does not matter which points we choose.
In fact, nearly every person is intimately familiar with this representation of projective space! Imagine that it is a clear night and you go out to look at the stars. You catch sight of the familiar constellation Orion, the hunter. The stars marking Orion's shoulders are Betelgeuse and Bellatrix, which we perceive to be neighboring stars that connect to form the figure of Orion. In fact, however, Betelgeuse is between two and three times as distant as Bellatrix. When we look up at the sky, we do not perceive the true three-dimensional space but points of light etched into the inner surface of the celestial sphere passing overhead. Stars in similar directions, regardless of their distances, are projected onto nearby points. This is why the result of treating all points along a line through the origin as equivalent is known as projective space.
It is clear, however, that every line through the origin intersects the sphere at exactly two points, while there can only be one representative for a point of projective space. Thus, by convention we consider only intersections with the upper hemisphere (just as in our example of the night sky - one cannot see stars looking downward!). This leaves only the "horizontal" lines intersecting the equator of the sphere twice. For these, we choose the points of intersection for positive y-values (the area colored dark green above) and finally the x-axis is represented by the dark red point of positive x. The projective plane is therefore the union of the yellow upper hemisphere, the dark green semicircle, and the dark red point. The latter two parts are the points at infinity.
The above image shows how the affine plane (and our first visualization) relate to our second visualization of the projective plane as (part of) a sphere. Lines through the origin (O) and a point in the upper hemisphere intersect the plane to form a one-to-one correspondence. As we would expect, points at infinity correspond to lines through the sphere's equator that are parallel to the plane and are therefore not part of our original affine plane.
Finally, the sphere illustrates how the projective plane solves the motivating problem of parallel lines than began this post.
Two parallel lines in the plane correspond to precisely the same lines in our first visualization, which indeed embeds a "copy" of the affine plane in three-dimensional space. When these parallel line are transferred to the sphere in the same manner that the point was above (remember: each transferred point represents a line through the origin and "transferring" a point is merely choosing a different representative), the figure above is the result. However, it is evident that the resulting arcs on the sphere intersect at the equator (green circle) and we know the equator contains the points at infinity! Though there appear to be two intersections, recall that points diametrically opposite from one another are on the same line through the center, so that these points are identified as one in the projective plane. We have our desired result: two parallel lines intersect in exactly one point.
The next post provides an algebraic description of the projective plane and explores more of its properties.
Sources: Algebraic Curves: An Introduction to Algebraic Geometry by William Fulton, https://www.math.toronto.edu/mathnet/questionCorner/qc_hlimgs1/image87.gif, http://jwilson.coe.uga.edu/EMAT6680Fa11/Chun/Final1/4.png, http://courses.cs.washington.edu/courses/cse557/98wi/readings/xforms/diagram/homogeneous.gif, http://earthsky.org/astronomy-essentials/how-far-is-betelgeusehttp://en.wikipedia.org/wiki/Projective_space
From this, we naturally comes the intuition that "parallel lines intersect at infinity." Certainly this tidies up our intersection statement because it provides a way for even parallel lines to intersect. But what does "at infinity" mean? Is there really a "point" there? The notion of projective space makes these ideas explicit and rigorous.
We focus on the (real) projective plane, the extension of the normal plane to include these "points at infinity" where parallel lines intersect. The set of points in the projective plane is defined, somewhat enigmatically, as "the set of lines through the origin in three-dimensional space." Defining each point to be a line in a different space seems extremely confusing at first, but there are multiple ways to visualize this concept.
The first method of visualization illustrates how the projective plane is related to the ordinary plane (sometimes called the affine plane). Consider three-dimensional space with ordinary coordinates x,y, and z as shown. The plane labeled z = 1 contains all points for which the z coordinate is 1, namely all those of the form (x,y,1). Clearly this plane is just like the ordinary two-dimensional plane (under the correspondence (x,y,1) → (x,y)), only embedded in three dimensions, like a flat sheet of paper in our world (but infinite). The dotted line shown that passes through the origin intersects the plane at the particular point (a,b,1). Remembering that the projective plane is meant to be an extension of the affine plane, we identify the dotted line with the point where it intersects the plane. Clearly, for each point in the z = 1 plane, there exists exactly one line through the origin and the given point. This shows how the ordinary plane is a subset of projective space (the set of lines through the origin)!
However, not every line through the origin intersects the plane z = 1. For instance, the x-axis, the y-axis (both shown), and any other line in the plane of these two axes only contain points for which the z coordinate is 0 and can never intersect the plane z = 1 (to be clear, the three-dimensional space considered here does not have its own points at infinity!). Therefore, these lines cannot correspond to points on the ordinary plane. These special lines, in fact, are the points at infinity in the projective plane.
The above visualization illustrates the connection between the projective plane and the affine plane. It also indicates that there are many points at infinity, one for each line through the origin "lying flat" in the xy-plane. However, it fails to indicate how points at infinity are truly the intersections of parallel lines. For this, we use another visualization that chooses different representative points.
Using a sphere (or a hemisphere, to be more precise) to represent the projective plane is just as legitimate as using a plane: all that matters is that there is one point for each line through the origin. It does not matter which points we choose.
In fact, nearly every person is intimately familiar with this representation of projective space! Imagine that it is a clear night and you go out to look at the stars. You catch sight of the familiar constellation Orion, the hunter. The stars marking Orion's shoulders are Betelgeuse and Bellatrix, which we perceive to be neighboring stars that connect to form the figure of Orion. In fact, however, Betelgeuse is between two and three times as distant as Bellatrix. When we look up at the sky, we do not perceive the true three-dimensional space but points of light etched into the inner surface of the celestial sphere passing overhead. Stars in similar directions, regardless of their distances, are projected onto nearby points. This is why the result of treating all points along a line through the origin as equivalent is known as projective space.
It is clear, however, that every line through the origin intersects the sphere at exactly two points, while there can only be one representative for a point of projective space. Thus, by convention we consider only intersections with the upper hemisphere (just as in our example of the night sky - one cannot see stars looking downward!). This leaves only the "horizontal" lines intersecting the equator of the sphere twice. For these, we choose the points of intersection for positive y-values (the area colored dark green above) and finally the x-axis is represented by the dark red point of positive x. The projective plane is therefore the union of the yellow upper hemisphere, the dark green semicircle, and the dark red point. The latter two parts are the points at infinity.
The above image shows how the affine plane (and our first visualization) relate to our second visualization of the projective plane as (part of) a sphere. Lines through the origin (O) and a point in the upper hemisphere intersect the plane to form a one-to-one correspondence. As we would expect, points at infinity correspond to lines through the sphere's equator that are parallel to the plane and are therefore not part of our original affine plane.
Finally, the sphere illustrates how the projective plane solves the motivating problem of parallel lines than began this post.
Two parallel lines in the plane correspond to precisely the same lines in our first visualization, which indeed embeds a "copy" of the affine plane in three-dimensional space. When these parallel line are transferred to the sphere in the same manner that the point was above (remember: each transferred point represents a line through the origin and "transferring" a point is merely choosing a different representative), the figure above is the result. However, it is evident that the resulting arcs on the sphere intersect at the equator (green circle) and we know the equator contains the points at infinity! Though there appear to be two intersections, recall that points diametrically opposite from one another are on the same line through the center, so that these points are identified as one in the projective plane. We have our desired result: two parallel lines intersect in exactly one point.
The next post provides an algebraic description of the projective plane and explores more of its properties.
Sources: Algebraic Curves: An Introduction to Algebraic Geometry by William Fulton, https://www.math.toronto.edu/mathnet/questionCorner/qc_hlimgs1/image87.gif, http://jwilson.coe.uga.edu/EMAT6680Fa11/Chun/Final1/4.png, http://courses.cs.washington.edu/courses/cse557/98wi/readings/xforms/diagram/homogeneous.gif, http://earthsky.org/astronomy-essentials/how-far-is-betelgeusehttp://en.wikipedia.org/wiki/Projective_space
Labels:
Mathematics
Subscribe to:
Posts (Atom)